Samadrita Ghosh, a Computer Science Engineer and Software developer, was always interested in how computers are programmed to think like humans, making human work easier and faster than ever. She took up modules like AI, ML, Cloud Computing, RDBS, and Theory of Computing in her last semester along with her Dissertation. Samadrita, apart from her Computer Science modules enjoys playing chess in her free time but does not always get a person who knows how to play the board game. Finally, she downloaded a chess application to play with the computer. She was amazed to discover how a machine with no human brain could defeat her and play smarter. Curiosity made her dig deeper into how chess is programmed into a computer thus her final year dissertation was a research paper on “Building a Chess application using backpropagation algorithm”.
Today Samadrita has joined us to speak about her research around backpropagation, inclusion of AI and Neural Networks and the future applications.
What is the N-Queen problem?
Samadrita: The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, the eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other.
Thus, a solution requires that no two queens share the same row, column, or diagonal.
So, what is Backpropagation?
Samadrita: In a 4-Queen problem, when we observe a Dead end, backtracking or backpropagation (going back to previous state) is the natural solution. Backtracking ease the searching process and overall time may reduce for that. A feasible solution of a 4-Queen Problem depends on the constraints of placing 4-Queens in respective rows. For example: Figure 1 is a feasible solution whereas Figure 2 is not a feasible solution. Backpropagation is the foundation of neural network training. The practice of fine-tuning a neural net’s weights depending on the error rate (i.e. loss) achieved in the preceding epoch (i.e. iteration). Proper weight adjustment ensures decreased error rates, boosting the model’s reliability and generalization.
|
X |
Q |
X |
X |
|
X |
X |
X |
Q |
|
Q |
X |
X |
X |
|
X |
X |
Q |
X |
Figure 1
|
Q |
X |
X |
X |
|
X |
X |
X |
Q |
|
X |
Q |
X |
X |
|
X |
X |
X |
X |
Figure 2: No place to put any queen on 4th row.
What is a Neural Network for chess?
Samadrita: There is a specific structure of neural networks. It is a network that starts with nodes, often known as neurons. These neurons are often arranged into tiers. Each network has at least one input and output level. There are generally several hidden layers between input and output. Neurons on one level link to neurons on the next level. There are several techniques of organising these links. However, she supposes that each neuron on one level is linked to all neurons on the next level.
The task of the network should be to evaluate a chess position as well as possible.
The path from a minimal neural network to a network that can evaluate the entire range of chess positions would be far too long and too complex. I will give you a simple example, the mating sequence of king and rook against king. Sounds simple, but let’s take a look at the following position:
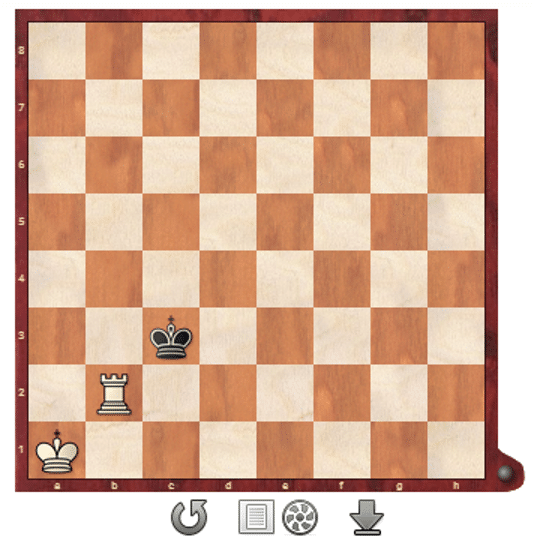
Figure 1: Position king and rook against the king (mate in 32 half moves)
It takes 16 moves (32 half moves) to mate with the best play from the starting position. Even with decent hardware, setting this search depth in an engine with a conventional search algorithm would result in an extremely long wait time for the initial move.
If the search depth is reduced, then a thorough position review must be done. After all, if onlythe material is counted, nothing would change because White would hold his additional rook even with random moves. Of course, there are recognized answers to this, such as additional points in the assessment if the Black king is near the board’s edge or if the White rook shuts off the king’s passage, and so on.
So what are the advantages and disadvantages of using the backpropagation algorithm in Neural Networks
Samadrita: The advantages of using a backpropagation algorithm is, no prior understanding of a neural network is required, making it simple to construct. It’s easy to program because there are no additional parameters besides the inputs. The backpropagation method alsoeliminates the need to understand the features of a function, which speeds up the process. Finally, the model’s simplicity makes it adaptable to a wide range of settings.
However, backpropagation is not a one-size-fits-all answer for all neural network-related problems. Some of the potential shortcomings of this paradigm are training data influencesmodel performance, thus high-quality data is necessary. Noisy data can also impair backpropagation, thereby tainting the results. Training and bringing backpropagation models up to speed might take some time. Backpropagation necessitates a matrix-based technique, which might lead to additional difficulties.
Thank you Samadrita, many thanks for your time and good luck for your future endeavors.




